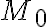|
Нехай у тривімірному просторі задана точка  і вектор і вектор  .Треба записати рівняння площини, що проходить через задану точку .Треба записати рівняння площини, що проходить через задану точку  перпендикулярно заданому вектору перпендикулярно заданому вектору 
Вибекремо на площині довільну (поточну) точку  , відмінну від , відмінну від 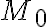 і розглянемо вектор і розглянемо вектор  . Яка б не була точка . Яка б не була точка  , оскільки вона лежитьв площині, вектор , оскільки вона лежитьв площині, вектор  буде перпендикулярним вектору буде перпендикулярним вектору  , який за умовою перпендикулярний площині, значить перпендикулярній будь-якому вектору, що в цій площині лежить. , який за умовою перпендикулярний площині, значить перпендикулярній будь-якому вектору, що в цій площині лежить.
З векторної алгебри відомо, що перпенликулярність двох ненульових векторів еквівалентна рівності до нуля їх скалярного добутку.
За умовою, координати вектора  є є  , а вектор , а вектор  своїми проекціями має різниці координат точок своїми проекціями має різниці координат точок  і і 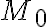

Знайдемо скалярний добуток цих векторів і прирівняємо його до нуля.

Остання рівність

і являє собою рівняння площини, що проходить через задану точку перпендикулярно заданому вектору.
Вектор  , перпендикулярний площині називається нормальним вектором цієї площини. , перпендикулярний площині називається нормальним вектором цієї площини.
|
 перпендикулярно вектору
перпендикулярно вектору  .
.