Математика-ВАВ ...

До лінійних об'єктів в тривімірному просторі, крім площини, відноситься і пряма. Як і площина, пряма в просторі однозначно визначається заданням точки і вектора.Точки, через яку пряма проходить, і вектора, що задає напрямок прямої. Оскільки вектор може вільно переміщуватись, можна вважати, що вектор лежить на прямій або він їх колінеарний. Такий вектор називається напрямлюючим вектором прямої.

Отримаємо рівняння прямої в просторі, що проходить через задану точку $M_0(x_0,\,y_0,\,z_0)$ в напряку, що задається вектором $\overline{a} = (a_x,\,a_y,\,a_z)$.

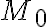Візьмемо на прямій поточну точку $M(x,\,y,\,z)$ і розглянемо вектор $\overline{M_0 M}$. Яка б не була точка $M$, оскільки вона, разом з точкою $M_0$, лежить на прямій, вектор $\overline{M_0 M}$ буде теж лежати на прямій. А це означає, що для будь-якої точки $M$ вектор $\overline{M_0 M}$ буде колінеарним вектору $\overline{a}$.

Використовуючи умову колінеарності векторів отримаємо рівняння

$\large{\frac{x-x_0}{a_x}=\frac{y-y_0}{a_y}=\frac{z-z_0}{a_z}}$

які називаються канонічними рівняннями прямої в просторі.

Зауважимо, що вираз канонічні рівняння використовується в множині, оскільки наведене співвідношення містить два рівняння, що задають зв'язок між трьома змінними.

Наведемо найважливіший випадок використання канонічних рівнянь, а саме, отримаємо рівняння прямої в просторі, що проходить через дві задані точки.

Нехай маємо точки $M_{1} (x_{1},\,y_{1},\,z_{1} )$ і $M_{2} (x_{2},\,y_{2},\,z_{2} )$ і потрібно написати рівняння прямої, що проходить через ці точки.

Оскільки точка $M_{1}$ лежить на прямій, рівняння шуканої прямої можна записати у вигляді

$\large{\frac{x-x_1}{a_x}=\frac{y-y_1}{a_y}=\frac{z-z_1}{a_z}}$, (1)

де $\overline{a} = (a_x,\,a_y,\,a_z)$ напрямлюючий вектор прямої. Оскільки і точка $M_{2}$ лежить на прямій, вектор $\overline{M_1 M_2}$ буде теж лежати на нашій прямій. Це означає, що його можна прийняти за напрямлюючий вектор прямої. Знайдемо його координати, як різниці відповідних координат точок кінця і початку, після чого підставимо їх в рівняння (1). Маємо:

$\overline{M_1 M_2}=(x_2-x_1,\,y_2-y_1,\,z_2-z_1)$,

Тоді

$\large{\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}}$.

Останні рівняння і являють собою канонічні рівняння прямої, що проходить через дві задані точки.

Зауваження.

Канонічні рівняння являють собою лише формальний запис, що характеризує перну пряму в просторі. Тому припустимо ставити навітть нуль в знаменнику дробу, що входить в рівняння. Так рівняння

$\large{\frac{x-3}{4}=\frac{y-1}{0}=\frac{z-2}{5}}$.

описує пряму, що проходить через точку (3,1,2) і лежить в площині $y=1$, тобто паралельну площині $XOZ$ .