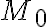6.7. Параметричні та векторне рівняння прямої.
Крім канонічних та загального рівняння прямої в просторі іноді зручно користуватись параметричними або векторним рівнянням, з якими ми зараз і познайомимося.
Нехай маємо канонічні рівняння прямої
що проходить через точку  з напрямлюючим вектором
з напрямлюючим вектором  .
.
Рівняння являють собою рівності між трьома відношеннями. Якщо обрати довільну точку  на прямій і підставити в рівняння її координати замість змінних, кожне з відношень прийме певне значення, причому, виходячи з рівняння, всі ці значення будуть співпадати між собою. Позначими спільне значення всіх трьох дробів через
на прямій і підставити в рівняння її координати замість змінних, кожне з відношень прийме певне значення, причому, виходячи з рівняння, всі ці значення будуть співпадати між собою. Позначими спільне значення всіх трьох дробів через  . Маємо
. Маємо
Останній вираз еквівалентий трьом рівнянням.
Або, після певних перетворень, приходимо до параметричних рівнянь прямої
Кожній точці прямої відповідає певне значення параметра, і навпаки, кожне значення параметра однозначно визначає певну точку прямої. Так, значенню  відповідає точка
відповідає точка  .
.
Щоб отримати векторне рівняння, розглянемо три вектори:
 - радіус-вектор поточної точки
- радіус-вектор поточної точки  ;
;

Координати радіус-векторів точок співпадають з координатами цих точок, тому можна написати  і
і  . Вектор же
. Вектор же  колінеарний напрямлюючому вектору
колінеарний напрямлюючому вектору  , тоді
, тоді