Математика: 7.4. Границя послідовності.

7.4. Границя послідовності.

В цьому пункті ми розглянемо основне поняття, пов'язане з послідовностями - поняття границі.

Означення 1.
Число

$a$ називається границею послідовності

$\;\{x_n\}$ , якщо для будь-якого, скіль завгодно малого, додатнього

$\varepsilon$ знайдеться такий номер

$N$ , що всі елементиы з номерами

$n$ більшими за

$N$ :

$n\;\ge\;N$ , відстоять від числа

$a$ менше, ніж на

$\varepsilon$ .

$|x_n-a|\lt \varepsilon$
Границя послідовності позначається так:

$a=\lim\limits_{n \to \infty}x_n$
З використанням кванторів

$\forall \varepsilon \gt 0\; \exists N \; \forall n \ge N : |x_n\;-\;a|\lt\varepsilon \;\Rightarrow\;a=\lim_{n \to \infty}x_n$

Якщо послідовність має границю, вона називається збіжною.
Перш, ніж перейти до прикладів дамо ще одне, еквівалентне попередньому, означення границі послідовності.

Означення 2.
Околом точки

$a$ називається будь-який відкритий інтервал з центром в цій точці.
$\varepsilon$ -околом точки

$a$ називається інтервал довжиною

$2\varepsilon$ з центром в цій точці.

$(a-\varepsilon,\;a+\varepsilon)$ .

Означення 3.
Число

$a$ називається границею послідовності

$\;\{x_n\}$ (

$a=\lim_{n \to \infty}x_n$ ), якщо для будь-якого, скіль завгодно малого, додатнього

$\varepsilon$ знайдеться такий номер

$N$ , що всі елементи послідовності, починючи з

$x_N$ містяться в

$\varepsilon$ -околі точки

$a$ .

Приклади.

1. Послідовність

$\{x_n\}=\{1,\;\frac{1}{2},\;\frac{1}{3},\;\frac{1}{4},\;\frac{1}{5},\;\dots,\; \frac{1}{n},\;\dots\}$
має границею 0:

$\lim_{n \to \infty}\frac{1}{n}=0$
Це означає, що наскільки б маленьким ми не взяли

$\varepsilon$ , скажімо,

$\varepsilon=0,001$ , все одно знайдеться достатньо великий номер

$N$ (для нашого

$\varepsilon=0,001$ таким номером буде

$N=1001$ ), такий що для всіх

$n\;\ge\;N$
величина

$\frac{1}{n}$ буде менше за

$\varepsilon$ , тобто

$\frac{1}{n}$ буде ближче до 0, чім

$\varepsilon$ . Дійсно, і

$\frac{1}{1002}$ , і

$\frac{1}{1003}$ і всі наступні елементи послідовності будуть менші за

$\varepsilon$ , тобто відстоять від 0 менше, ніж на

$\varepsilon$ , а це і означає, що 0 є границя цієї послідовності.

2. Границя послідовності

$\{x_n\}=\{0,\;\frac{1}{2},\;\frac{2}{3},\;\frac{3}{4},\;\frac{4}{5},\;\dots,\; \frac{n-1}{n},\;\dots\}$
дорівнює 1:

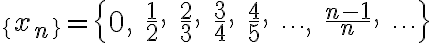
$\lim_{n \to \infty}\frac{n-1}{n}=1$
Дійсно, для обраного

$\varepsilon \gt 0$ візьмемо

$N \gt \frac{1}{\varepsilon}$ . Тоді для всіх

$n\;\ge\;N$ маємо

$x_n=\frac{n-1}{n}=1-\frac{1}{n}\gt 1-\frac{1}{\frac{1}{\varepsilon}}\;=\;1-\varepsilon$ .

Починаючи з

$x_N$ всі елементи послідовності відстоять від 1 менше, ніж на

$\varepsilon$ , тобто якраз 1 і є границею послідовності

$x_n=\frac{n-1}{n}$ .

Зазначимо, що номер $N$ , взагалі кажучи, залежить від $\varepsilon$ , як правило, чим менше $\varepsilon$ , тім більший номер $N$ доводиться обирати. Але, щоб границя існувала, необхідно, щоб для кожного $\varepsilon$ відповідаючий йому номер все ж таки знайшовся.

3. Границя сталої послідовності

$\{c\}=\{c,\;c,\;\dots,\;c,\;\dots\}$ дорівнює числу с, оскільки всі елементи послідовності завідомо знаходяться в будь-якому, скіль зівгодно малому околі точки с.

$\lim_{n \to \infty} c=c$
4. Границя послідовності

$\{n^2\}=\{1,\;4,\;9,\;16,\;\dots,\; n^2,\;\dots\}$ взагалі не існує. Яке б число ми ни спробували б узяти в якості границі, елементи послідовності

$x_n\;=\; n^2$ , прямуючи в нескінченість, не зможуть знаходитись в малому околі цього числа.

Last modified: Sunday, 18 September 2016, 11:12 PM