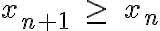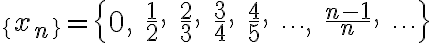7.7.Монотонні послідовності. Число е.
Якщо послідовність має границю, то вона обмежена, але не кожна обмежена послідовність має границю. В той же час, існує умова, яка, разом з обмеженістю, гарантує збіжність послідовності.
Означення.
Послідовність  називаєтся монотонно зростаючою, якщо кожний її навтупний елемент більше за попередній: називаєтся монотонно зростаючою, якщо кожний її навтупний елемент більше за попередній:  . .
Аналогічно, послідовність  називаєтся монотонно спадаючою, якщо для будь-якого називаєтся монотонно спадаючою, якщо для будь-якого  виконується виконується 
Якщо в определении замінити строгі нерівеності на нестрогі, то отримаємо неспадаючу (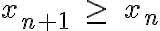 ) або незростаючу ( ) або незростаючу ( ) послідовність. ) послідовність.
Послідовності, що задовільняють будь-яку з наведених вище умов, називаються монотонними.
Приклади.
1.Послідовність  монотонно зростає. монотонно зростає.
2.Послідовність

монотонно спадає.
3.Послідовність  взагалі не монотонна. взагалі не монотонна.
|
Теорема.
Монотонно зростаюча обмежена зверху числом  послідовність послідовність  має границю, і ця границя не перебільшує числа має границю, і ця границя не перебільшує числа 

Монотонно спадаюча обмежена знизу числом  послідовність послідовність  має границю, при цьому має границю, при цьому

Зауваження.
В теоремі строге зростання або спадання можна замінити на неспадання і незростання.
Приклад.
Послідовність
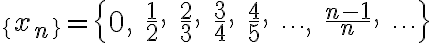
монотонно зростає і обмежена зверху одиницею, оскільки дріб  завжди строго менше одиниці. завжди строго менше одиниці.
Ця послідовність має границю

. |
Число е.
Найважливішим прикладом використання наведеної теореми є означення числа е - основи натурального логарифма, - через границю послідовності.
Розглянемо послідовність

Можна довести, що ця послідовність, з одного боку, строго зростає, а з іншого, обмежена числом 3:  . Тоді ця послідовність має границю, що також не перебільшує 3. Число, до якого прямує ця послідовність позначається е. . Тоді ця послідовність має границю, що також не перебільшує 3. Число, до якого прямує ця послідовність позначається е.

Число е відіграє найважливішу роль в математичному анализі і інших розділах вищої математики. Відмітимо, що число е ірраціональне і, з точністю до 9 знаків дорівнює

В грубих розрахунках можно прийняти  . . |
Zuletzt geändert: Monday, 19. September 2016, 14:31